Intro

데이터베이스는 빠른 데이터 탐색을 위해 인덱스를 이용한다. 인덱스는 특정 키에 대해 레코드 id 혹은 레코드 그 자체를 정렬한 자료 구조로
주로 B+ tree를 이용해 구현한다. B+ tree는 Balanced Tree를 위해 고안된 B-tree 알고리즘을 발전시킨 버전으로 왜 B+ tree를 사용하는지, 그리고
B+ tree의 concurrency를 높이기 위해 어떤 방식으로 잠금(Lock)을 수행하는지 알아보자.

Binaray Search Algorithm

무작위로 늘어진 데이터 속에서 원하는 조건의 데이터를 찾는 것은 매우 힘든 일이다. 모든 데이터를 하나씩 살펴보며 주어진 조건이 나올 때까지 탐색해야하며, 만약 중복키가 허용될 경우
무조건 모든 데이터를 한번씩 살펴봐야 한다. 따라서 $O(N)$의 높은 시간복잡도가 필요하다.

가장 기본적인 아이디어는 데이터가 정렬되어 있다고 가정하는 것이다. 그러면 만약 내가 현재 보고 있는 값이 원하는 값보다 크거나 작은지 여부에 따라 앞으로 이동할지 뒤로 이동할지 선택가능하다.
그러면 한칸씩 이동할까? 아니면 몇칸씩 이동해야할까? 한칸씩 이동하는 것은 무작위 데이터를 살펴보는 것과 거진 다를 바 없는 무식한 방법이다. 따라서 여러칸을 이동해야 함은 자명하다.

가장 합리적인 선택이 무엇일까 하면 남은 길이의 절반만큼 건너뛰는 것이다. 절반만큼 건너뛰고 나서 다시 비교해보고 값이 같으면 거기서 멈추고, 다시 크거나 작은지 여부에 따라 앞으로 갈지 뒤로 갈지 정하는 것이다.

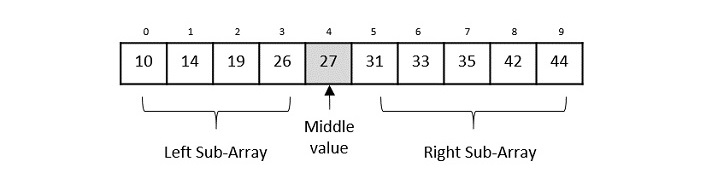
Binary Search Algorithm은 이러한 아이디어를 이용한 방법으로 정중앙에서부터 탐색을 시작한다. 만약 값이 더 작거나 크다면, 앞의 절반 혹은 뒤의 절반만 탐색해도 충분하다는 것이 결론.
이러한 방식에 따라 탐색해야 하는 범위는 매번 절반씩 줄어들며, 전체 개수가 유한하니 탐색 범위도 유한번의 탐색 안에 반드시 1로 수렴한다. 시간복잡도는 $O(\log{N})$.

n-ary Search는 단지 구간을 좀 더 늘려보자는 것이다. Binary Search는 2개로 구간을 나누었고, n-ary는 n개로 구간을 나누는 차이다.

탐색시간이 더 짧은 방식도 있을까? 생각해보면 있긴 하다. 바로 Hash를 이용하는 것이다. Hash collosion 등의 다른 문제들을 무시하면 이 경우 탐색 시간이 $O(1)$이므로 매우 사기적이라 할 수 있다.

그럼에도 데이터가 정렬된 그 자체로 커다란 이점이 하나 있는데 바로 **범위 탐색(range scan)**이 가능하다는 점이다. Hash 키가 아주 이상적으로 뺵빽하게 차있다면 두 자료 구조 모두 시간복잡도가 동일하지만,
실제로는 매번 Hash 함수를 계산하기 위한 비용도 있을 거니와 없는 키에 대해서 범위 탐색을 하는 비용이 발생하기 때문에 비효율적이다.

다만 아직 문제가 되는 것이 하나 있는데 데이터를 추가, 삭제하는 비용이 너무 크다는 점이다. 기본적으로 정렬된 배열에 새로운 데이터를 추가하려면 1. 삽입될 위치를 확인하고 2. 데이터들을 한칸씩 뒤로 미루어야 하니 시간 복잡도가 $O(N)$이 소요된다. 삭제도 마찬가지. 따라서 이러한 이점을 유지하면서도 삽입과 삭제 효율을 높일 수 있는 방법을 고민해야 한다.

Binary Search Tree

Binary Search Tree는 기존의 단순한 정렬 배열에서 삽입과 삭제도 좀 더 효율적으로 수행하기 위해 고안된 자료구조이다.

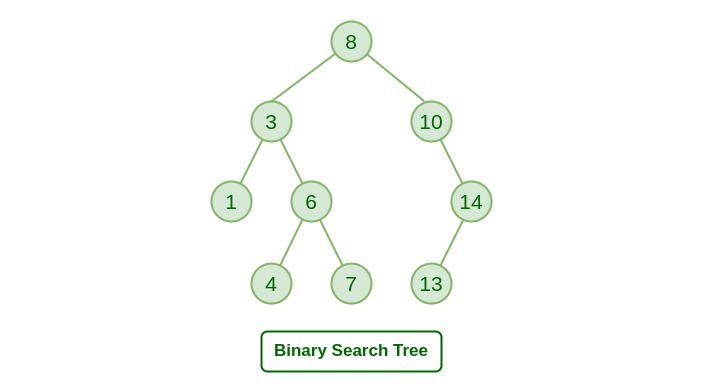
아이디어 자체도 상당히 직관적인데 트리의 노드에는 값이 담겨 있고 왼쪽 자식은 더 작은 값, 오른쪽 자식은 더 큰값으로 가는 경로를 가리킨다.
따라서 탐색도 Binary Search와 거의 똑같은 방식으로 이루어지는데, 루트 노드에서부터 시작해서 노드의 값을 비교해서 왼쪽, 혹은 오른쪽 자식 노드로 나아가며 원하는 값을 찾을 수 있다.
범위 탐색의 경우, 중위순회와 가지치기를 통해 불필요한 계산 없이 수행할 수 있다.

그럼 삽입과 삭제는?
삽입은 매우 단순하다. 탐색과 똑같이 리프노드로 접근한다음 리프노드보다 더 작으면 왼쪽 자식으로, 더 크면 오른쪽 자식으로 추가한다.

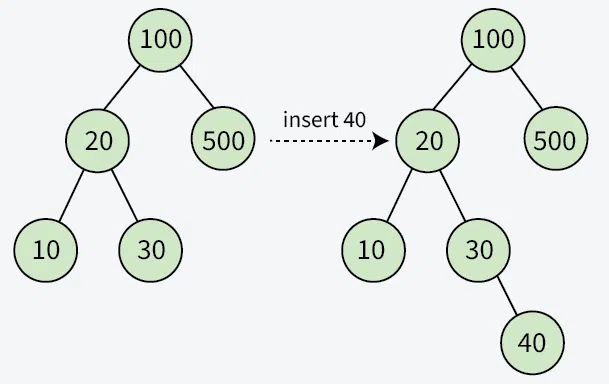
삭제의 경우는 쪼오금 복잡한데,

1. 만약 대상 노드가 리프노드일 경우 그대로 삭제한다.
2. 만약 대상 노드가 자식을 한 개만 가지고 있을 경우 대상 노드를 자식노드 값으로 대체하고 자식 노드가 삭제된다.(높이 감소)
3. 만약 대상 노드가 두 자식을 모두 보유하고 있으면, inorder successor 혹은 inorder predecessor와 대상 노드 값을 교체하고 삭제한다.

여기서 inorder successor와 inorder predecessor는 복잡하게 말하면 "중위 순회(inorder traverse)을 통해 직전 혹은 직후에 탐색하는 노드"라고 할 수 있고,
값으로선 대상노드와 가장 가까운 두 값을 담은 노드라고 할 수 있다. 그림으로 보면 더 직관적이다.

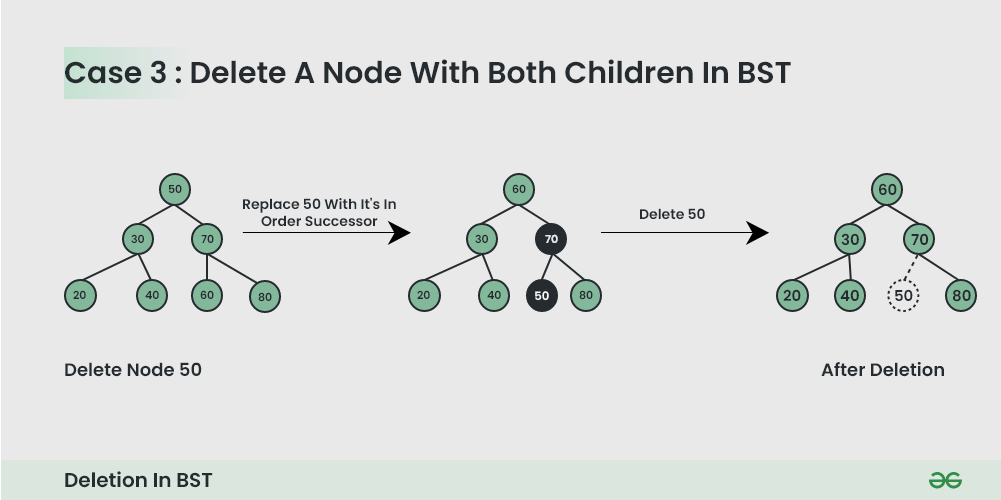
그림의 경우 오른쪽 서브트리의 가장 왼쪽 리프노드를 삭제하는 과정을 보여준다.

이 경우 시간 복잡도는 어떻게 될까? 이상적으로는 탐색, 삽입, 삭제 모두 $O(\log(N))$의 시간복잡도를 가진다.
이는 트리가 균형을 이루었다는 가정으로 모든 노드의 양쪽 서브트리에 균등하게 데이터가 배분되었을 경우 매 탐색마다 범위가 2배씩 줄어들기 때문이다.

다만 최악의 경우는 $O(N)$이 되는데, 이는 트리가 극단적으로 한쪽에만 모든 원소가 배분되었을 경우이다. 이 경우 트리는 연결리스트와 다를바 없는 상태가 되어 탐색에 아무런 이점을 얻을 수 없다.
이런 케이스가 일어날 수도 있을까? 순서대로 데이터가 삽입되면 가능하다. 1부터 100까지 순서대로 삽입하면 루트노드는 1이고 모든 자식은 오른쪽에만 연결되어 극단적으로 불균형한 트리가 생성된다.

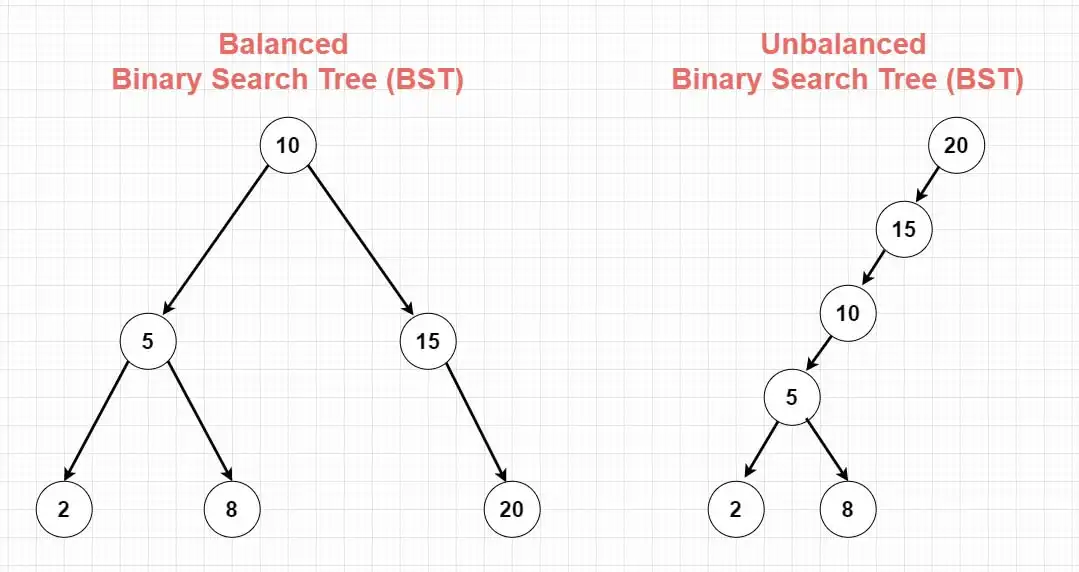
따라서 다음 목표는 어떻게 하면 트리가 최대한 "균형상태"를 유지할 수 있도록 하는가? 가 된다.

B-Tree, B+-Tree

Balanced Tree는 앞서 말한 균형상태를 유지하기 위한 목적으로 설계된 알고리즘으로 여러가지 종류가 있다.
B-Tree는 n-aray balanced tree(다진 균형 트리)를 위한 알고리즘으로 한 노드에 여러가지 값을 저장하고 여러 자식을 가지는 트리이다.
B+-Tree는 B-Tree에서 범위탐색 효율을 더 높인 알고리즘으로 리프노드에만 실제 값을 저장하고 부모노드는 모두 범위를 구분하는 역할만 수행한다.
탐색 과정 자체는 앞서 살펴본 Binary search, n-ary search와 똑같다.

이러한 다진 균형 트리는 데이터베이스에서 가장 흔히 사용되는 자료 구조인데, 굳이 이진트리가 아니라 다진트리를 구성하는 이유는 디스크 IO 비용을 줄이기 위함이다.

보통 데이터베이스에서는 페이지 하나에 트리 노드 하나를 할당하는데, 이는 페이지 단위로 락이 제어되기 때문이며,
만약 한 페이지에 여러 노드가 저장되어 있으면 노드 하나를 탐색하기 위해 불필요한 노드까지 접근이 제한되어 동시성에 손해가 된다.

이 때 한 노드에 적은 값이 저장되면 그만큼 트리 전체의 밸런스를 유지하기 위한 연산이 더 자주 발생하여 여러 노드에 자주 접근해야 하고, 이는 곧 디스크 IO 비용이 증가함을 의미한다.

이제 간단히 B-Tree와 B+-Tree가 균형을 유지하는 방식에 대해 알아보자.

삽입과 분할

트리가 불균형 상태에 빠질 수 있는 잠재적인 상황은 당연히 삽입과 삭제이다. B-tree는 삽입의 경우 분할(Split), 삭제의 경우 **재분배(Redistribution)와 병합(Merge)**를 통해 트리 균형을 회복하는데, 하나씩 살펴보자.

기본적으로 B-Tree 삽입은 현재 삽입하려는 값에 대응되는 리프노드에 먼저 값을 삽입한다. 이 때 트리가 불균형 상태가 될 수 있는 케이스는 리프노드가 이미 꽉차서 새로운 하위 노드를 추가해야하는 경우이다.
이 때 B-Tree는 하위 자식을 추가하는 것을 막기 위해 옆으로 새로운 자식(형제노드)을 추가한다. 이 때 기존 노드에서 절반 값을 형제에게 "분할"하여 두 노드가 최대 크기의 절반만큼 값을 분배하는 것이다.

여기까지 OK. 그러면 이걸로 끝인가? 그렇지 않다. 형제 노드에게 접근하기 위해선 부모도 형제의 존재를 알아야 한다. 따라서 분할 시점에 대상 노드의 중앙값과 형제노드 포인터를 부모 노드에 삽입하며, 중앙값을 기준으로 왼쪽 구간과 오른쪽 구간을 형제끼리 나누어 가진다.

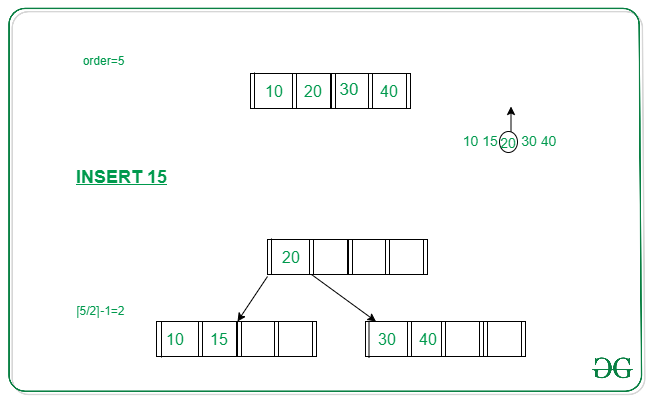
그런데 만약 부모도 꽉차있다면? 또 부모 노드에 대한 분할을 수행한다. 여기서도 똑같이 중앙값을 부모의 부모 노드로 삽입하고 ...
이런 과정을 반복하다 루트 노드에 도달했다고 가정하자. 루트 노드도 꽉차있으면 어떡할까? 이 때 트리의 높이가 증가한다. 새로운 루트 노드를 생성하고, 중앙 값을 기준으로 값을 분배하고...

이러한 삽입 과정에서 소요되는 시간복잡도는 리프노드 탐색 $O(\log(N))$ + 최대 $\log(N)$번의 분할이 발생하고 각 분할에서는 노드의 최대 원소 개수가 $M$일 때 $M/2$개의 값을 이동시킨다.
이 때 $M$의 경우 고정된 상수이고, 비교적 작은 값이기 때문에 적당히 무시하면 반드시 $O(\log(N))$ 시간 안에 삽입 과정이 완료된다.

삭제와 재분배, 병합

삭제의 경우 조금 더 복잡해진다.
B-Tree는 전체 트리의 높이가 너무 높아지는 것을 방지하기 위해 각 노드에 최소개수 제약조건을 부여하는데 이는 보통 $M/2$로 구성된다. 이 때 올림과 내림 여부는 구현에 따라 조금씩 달라지는 편.
따라서 분할상황에서도 최소개수 제약조건이 망가지지 않는다.

먼저 삭제 대상이 리프 노드에 존재하는 경우를 생각해본다.

1. 삭제하더라도 최소개수를 충족할 경우 그냥 삭제하면 끝.
2. 만약 최소개수를 충족하지 못할 경우... 양쪽 형제로부터 필요한 만큼 원소를 재분배하고, 만약 실패하면 병합

이 때 재분배는 형제 노드가 분배할 수 있을만큼 충분한 개수를 가지고 있어야 수행하며, 만약 불가하면 병합을 진행한다.
병합의 경우 부모노드의 원소를 하나 내리면서 진행하는데, 이 때 부모 노드의 개수가 부족해지면 bottom-up 방식으로 재분배 혹은 병합을 진행하며 올라간다.

만약 삭제대상이 부모 노드에 존재하는 경우, 해당 값을 inorder successor 혹은 inorder predecessor와 교체하고 교체된 리프노드를 삭제하며 똑같이 재분배 혹은 병합을 위로 올라가며 진행한다.

마찬가지로 삭제시간도 $O(\log(N))$안에 해결되는 것을 알 수 있다.

B+-Tree

B+-Tree는 무엇을 개선한 것일까? B-Tree와 거의 비슷하지만, 앞서 말했듯 리프노드에만 실제 값을 정렬하고 부모 노드는 모두 범위 구분을 위한 경계선 역할만 수행한다.
또한 B+-Tree의 리프노드는 형제노드와 연결리스트로 연결되어있다. 따라서 범위 탐색을 위해 매번 부모값을 방문하지 않아도 된다.

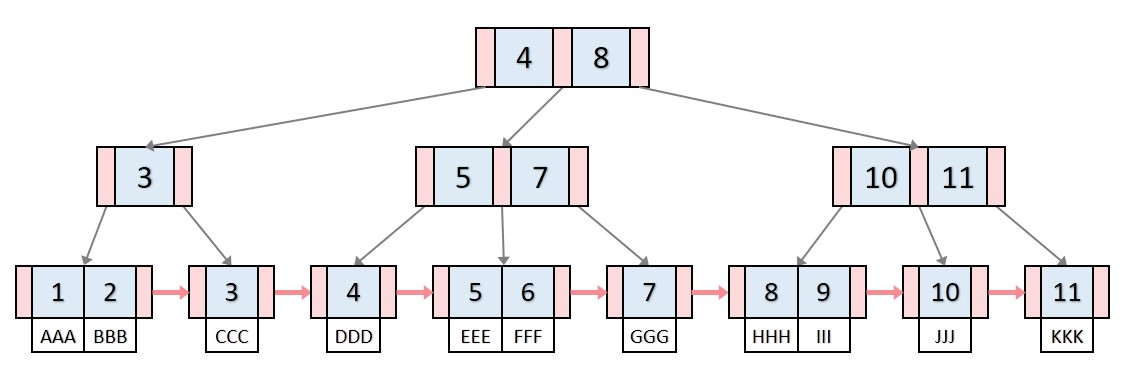
이러한 연결리스트를 통해 범위탐색이 간단해지는 것 같긴 한데 구체적으로 어디서 큰 이점이 있는지 잘 감이 안온다.
도리어 매번 리프노드까지 무조건 접근해야 하므로 오히려 손해보는 부분도 생기는 것 같고..
모든 페이지(노드)를 락으로 관리 하기 때문에 B+-tree가 명확히 이점을 가지게 된다.

가장 기본적으로 동시접근에서 트리를 보호하기 위해선 모든 인덱스 읽기/쓰기 작업에서 트리 전체가 락으로 보호해야 할 것이다.
그러나 이는 당연히 불필요한 노드까지 다른 스레드의 접근을 제한하기 때문에 최소한의 락을 획득하기 위해 모든 노드(페이지)의 락이 개별적으로 관리된다.

만약 B-tree를 통해 데이터를 관리한다고 가정해보자. 범위 탐색을 통해 일정 범위의 데이터를 탐색하면 어떻게 락을 관리해야 할까?
그 때 그 때 읽는 데이터만 락을 유지한다면 좀 곤란해진다. 만약 어떤 스레드는 위에서 아래로 내려오고 있는데 지금 범위 탐색을 하는 스레드는 자식에서 부모로 올라가고 있을 수 있다.
그러면 서로 락을 획득하기 위해 경합하며 데드락에 빠질 수 있는 위험이 있다.

그렇다고 필요한 범위의 모든 락을 유지하는 것도 쉽지 않다. 기본적으로 해당 범위에 속한 노드는 이미 탐색이 끝난 노드도 부모 노드에 락이 걸려있어 사실상 접근이 제한될 수 있다. 나중에 접근할 노드도 너무 일찍부터 접근이 제한될 수 있다.

그런데 B+-tree는 기본적으로 모든 리프가 연결되어있으니, 현재 탐색할 대상인 노드를 제외하면 굳이 락을 걸 필요가 없다. 따라서 그때그때 필요한 노드만 접근을 제한하여 효율적으로 범위를 탐색할 수 있는 것이다.

Lock Crabbing

B+-tree 접근에 있어 어떻게 잠금을 관리하는지 조금 더 생각해보자.
어쨌건 목표는 트리 자료 구조가 동시접근에서 보호되면서도 "꼭" 필요한 노드만 잠금을 걸어 접근을 제한하여 최대한 많은 스레드가 트리에 접근가능하도록 해야 한다.

Lock Crabbing은 마치 게들의 움직이는 모습처럼 락을 관리하는 정책으로 더이상 필요하지 않은 잠금은 즉시 해제하는 것을 목표로 한다.

먼저 키 검색 상황을 생각해보자.
모든 탐색은 반드시 부모를 거쳐 자식으로 내려가는 top-down 방식이다. 그러면 먼저 부모노드의 읽기락을 획득해야만 한다.
이제 자식노드의 위치(pointer)를 안전하게 탐색할 수 있다. 자식노드의 위치도 찾았다. 그럼 이제 부모노드에서 필요한 정보를 수집했으니 즉시 락을 풀고 자식노드의 락을 획득하면 될까?
아직 그렇지 않다. 부모노드 락을 해제하는 순간 다른 스레드도 부모노드에 접근하고 바로 동일한 자식노드에 접근할 수 있다. 심지어 현재 스레드보다 먼저!

T1: acquire_shared_lock(root)
T1: p <- search_child_pointer(root, key)
T1: release_shared_lock(root)
T2: acquire_shared_lock(root)
T2: p <- search_child_pointer(root, key)
T2: release_shared_lock(root)
T2: acquire_shared_lock(node[p])
T2: smo(...) // 병합, 분할 등으로 대상 리프가 다른 자식으로 넘어가버리면..

따라서 부모노드의 락을 해제하기 전에 먼저 자식노드 락을 획득해야만 안전하다.
이제 자식노드 아래의 서브트리가 모두 보호되고 있으니 부모노드는 더이상 락을 유지할 필요가 없으므로 해제해도 된다.
요약하면

1. 부모 노드에 대해 shared lock 획득
2. 자식 노드에 대해 shared lock 획득
3. 부모 노드 lock release.

그럼 삽입, 삭제 과정은 어떨까?

이 경우에는 우선 모든 노드에 대해 exclusive lock을 획득해야 할 것이다. 또한 분할, 병합, 재분배와 같은 연산은 모두 부모 노드와 함께 데이터가 변경되므로 부모노드의 락을 항상 해제할 수도 없다.
따라서 삽입, 삭제에서는 분할, 혹은 병합의 경우 최대 "한 개"의 원소를 삽입 혹은 삭제한다는 점에 착안한다.

만약 삽입 과정에서 트리를 타고 내려가던 중 현재 노드가 최대원소 개수라면, 추후 분할 상황에서 연쇄적인 분할의 대상이 될 수 있다. 하지만 적어도 한 개의 여유공간을 가지고 있다면 추후 연쇄적인 분할로부터 "안전"한 상태라는 의미가 된다. 즉, 현재 노드 이전의 부모들은 더 이상 삽입 과정에 의한 영향을 받을 일이 없다는 것이다.

삭제의 경우도 마찬가지인데, 만약 현재 개수가 최소개수 이하라면 추후에 발생할 수 있는 잠재적인 병합 상황에서 현재 노드도 연쇄적 병합의 대상이 될 수 있다. 하지만 적어도 한 개 더 많은 원소를 가지고 있다면, 적어도 연쇄적인 병합이 현재 노드에서 "끝"날 것이란 점이 보장된다.

따라서

1. 부모 노드에 대해 exclusive lock 획득
2. 자식 노드에 대해 exclusive lock 획득
3. 만약 자식 노드가 안전하면 자식 노드를 제외한 모든 조상 노드 lock release
4. 그렇지 않으면 부모 노드의 lock을 유지하고 계속 진행한다.

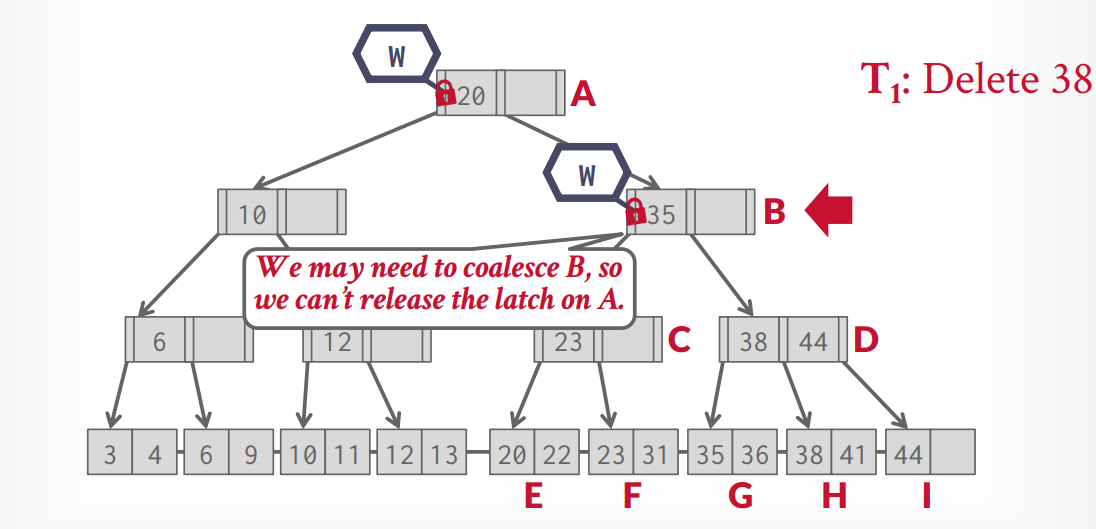
리프노드에서 범위 탐색할 경우도 잠금 획득은 비슷하게 작동한다. 현재 노드의 락을 획득한 상태에서 다음 형제의 락을 안전하게 획득하고 현재 노드의 락을 해제한다.

잠재적인 Deadlock

Range Scan으로 인해 잠재적인 데드락이 발생할 수 있는데, 이는 다음의 두 케이스이다.

1. 만약 리프노드가 양방향으로 연결된 구조일 때, 서로 반대 방향으로 범위 탐색을 진행하는 스레드.
2. 삭제 과정에서 Redistribution을 위해 형제노드의 락을 획득할 때, 범위 탐색이 형제 노드의 락을 획득하고 현재 노드로 진행(반대방향)하려는 경우.

두 경우 모두 서로 순환적으로 락을 획득하려다 보니 발생하는 문제이다.
그렇다고 해서 먼저 현재 노드 락을 해제할 경우 top-down과 비슷하게 문제가 되는데, 잠금 해제-잠금 획득의 간극 사이에 다음 형제노드 포인터가 변경될 수 있다.

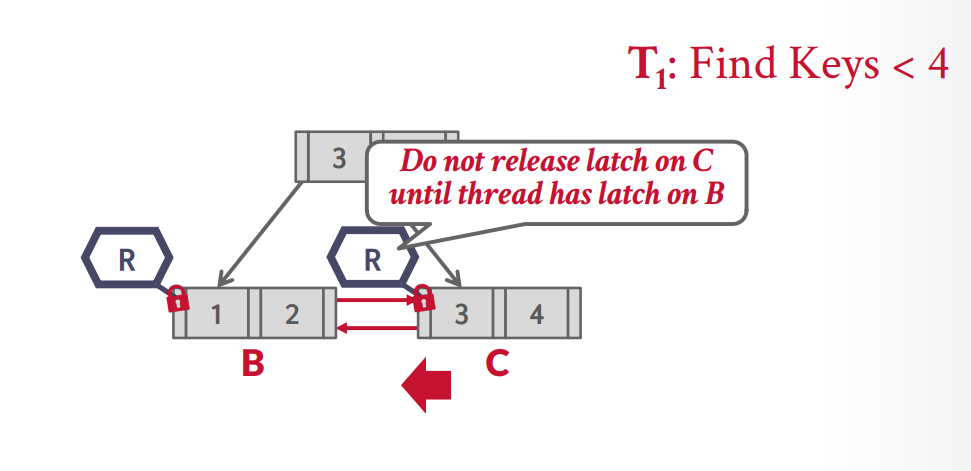
이런 케이스의 경우 안전한 잠금 순서를 유지하기 위해 단방향 연결리스트만 유지하는 방식으로 해결할 수 있다.
범위 탐색의 경우 반드시 앞에서 뒤로 나아가고, Redistribution도 반드시 오른쪽 노드와 수행하거나, 혹은 왼쪽 노드와 수행할 경우 현재 노드 락을 해제하고 왼쪽 노드 획득 - 현재 노드 재획득 순서를 통해
잠재적인 데드락의 가능성을 제거할 수 있다.

페이지 단위의 락은 latch라고 하는 좀 더 로우레벨 락으로 유지되기 때문에 deadlock detection 등의 기능이 지원되지 않는다.
따라서 만약 양방향 연결리스트를 유지할 경우, try_lock(=no-wait) 등의 방식을 통해 잠재적인 데드락을 방지한다.

낙관적 잠금 관리

삽입과 삭제 과정에서 B+-tree의 잠금을 관리할 경우를 다시 생각해보자.
부모노드에 대한 락을 거는 이유는 잠재적인 분할, 병합, 재분배에 대처하기 위함이다.

그런데 이러한 작업이 항상 일어나지는 않는다. 보통 노드 크기는 페이지를 최대한 채울 수 있을 정도로 구성하기 때문에,
작게는 몇십에서 많으면 몇백 몇천개까지 크기가 구성될 수 있다.

따라서 대부분의 삽입, 삭제에서 트리 구조변형은 드물게 일어나며 애초에 그 점이 다진트리의 이점이라 할 수 있다.
그러므로 "일단" 리프노드만 삽입, 삭제가 발생한다고 가정하고 락을 걸어보자는 것이다.

1. 탐색과정과 같이 shared lock을 통해 리프노드로 도달한다.
2. 리프노드에 도달하면 exclusive lock을 획득하고 리프노드의 현재 개수를 통해 분할, 병합 등이 필요한지 확인
3. 만약 SMO(분할, 병합 등)가 필요하면 리프노드 락을 해제하고 다시 루트부터 lock crabbing을 통해 내려온다.

만약 분할, 병합 등이 발생할 경우, 기존보다 더 많은 시간을 탐색에 소요해야 하지만 대부분의 삽입, 삭제는 루트와 부모 노드에 대해 shared lock을 통해 더 많은 스레드가 트리에 접근하도록 허용할 수 있다.

SMO first

통상적으로 SMO(Structure Modification Operation=Split, Merge, Redistribution)은 밑에서 위로 올라오는 bottom-top 순서로 수행된다.
이는 기본적으로 SMO의 비용이 비싸기 때문에 "꼭" 필요한 경우에만 수행하기 위함이다. 만약 부모부터 먼저 SMO를 수행했는데, 자식노드는 SMO가 필요 없다면 불필요한 작업을 한 셈이 된다.

그러나 낙관적 락 관리를 통해 부모부터 그 서브트리의 자식 줄기에 exclusive lock이 걸려있다고 가정해보자.
그러면, 이 때 보유한 노드들은 모두 SMO의 대상임이 반드시 보장된다. 왜냐하면 리프노드가 SMO가 필요하기 때문에 거기에 연쇄적으로 영향받을 부모들의 잠금을 다시 처음부터 모두 획득한 것이기 때문이다.

따라서 위에서 먼저 SMO를 수행하고 아래로 내려가는 것이 가능하다. 왜냐하면 어차피 나중에 해야할 일이니까.
이러면 더 빨리 부모노드의 락을 해제할 수 있다는 이점이 있는데, 내려갔다 올라오는 것보다 내려갔다가 다시 내려가면서 풀면 조금 더 빨리 다른 서브트리에 대한 접근이 가능하기 때문이다.

거기다 SMO를 먼저 수행하여 트리의 안정성을 보장할 경우 부모노드에 대한 제약조건을 조금 더 "느슨하게" 잡을 수 있다는 이점도 있다.
만약 아래에서 위로 올라오면, 실질적으로는 불안정한 노드를 판단하기 위해 최대 개수보다 -1개 혹은 최소개수보다 +1개 보유하고 있어도 잠재적인 분할/병합의 대상이 되어 잠금을 유지해야 하며
임계점에 도달하면 즉시 SMO를 수행해야 한다. 그러나 SMO를 먼저 수행함으로 인해 임계점에 도달하더라도 추후 꼭 필요할 때 분할/병합하여 조금 더 트리를 안정적으로 구성할 수 있다.

극단적으로는 노드의 최대 개수가 2인 트리에선 사실상 최대 개수가 1이냐 2냐의 문제가 되기 때문에 매우 큰 효과를 얻을 수 있다.