Published on

방대한 양의 데이터에서 count를 하는 법

Authors

Motivation

엄청난 트래픽이 발생하는 사이트에서 하룻동안 접속한 유저의 수를 집계하고 싶다고 가정해보자.
당연히 한 유저가 여러 번 요청을 발생시키니까 단순히 요청 수만 가지고 집계할 수는 없을 것이다.
정석적인 방법으로 이러한 집계를 하기 위해선 엄청난 메모리를 필요로 할 수 밖에 없다.

그렇다면 좀 더 효율적인 방식은 없는가?

HyperLogLog는 약간의 정확성을 손해보는 대신 근사적인 방법을 이용해 매우 낮은 메모리만으로도 집계를 할 수 있도록 만들어준다.
이를 이해하기 위해 간단한 예시부터 차근차근 나아가보자.

Cardinality(기수)는 집합의 개수를 세기 위한 개념으로 이 글에서는 고상하게 cardinality를 추정한다는 표현을 사용하겠다.

Simple Estimator

어떻게하면 효율적으로 데이터의 cardinality를 측정할 수 있을까?
확률을 이용한다.

Simple estimator는 hash의 성질을 이용한다. Hash function은 주어진 값을 어떤 범위 내의 랜덤한 값으로 맵핑한다.
이 때 Hash function의 대응은 보통 uniform distribution을 가지게 되는데 이를 이용해보는 것이다.

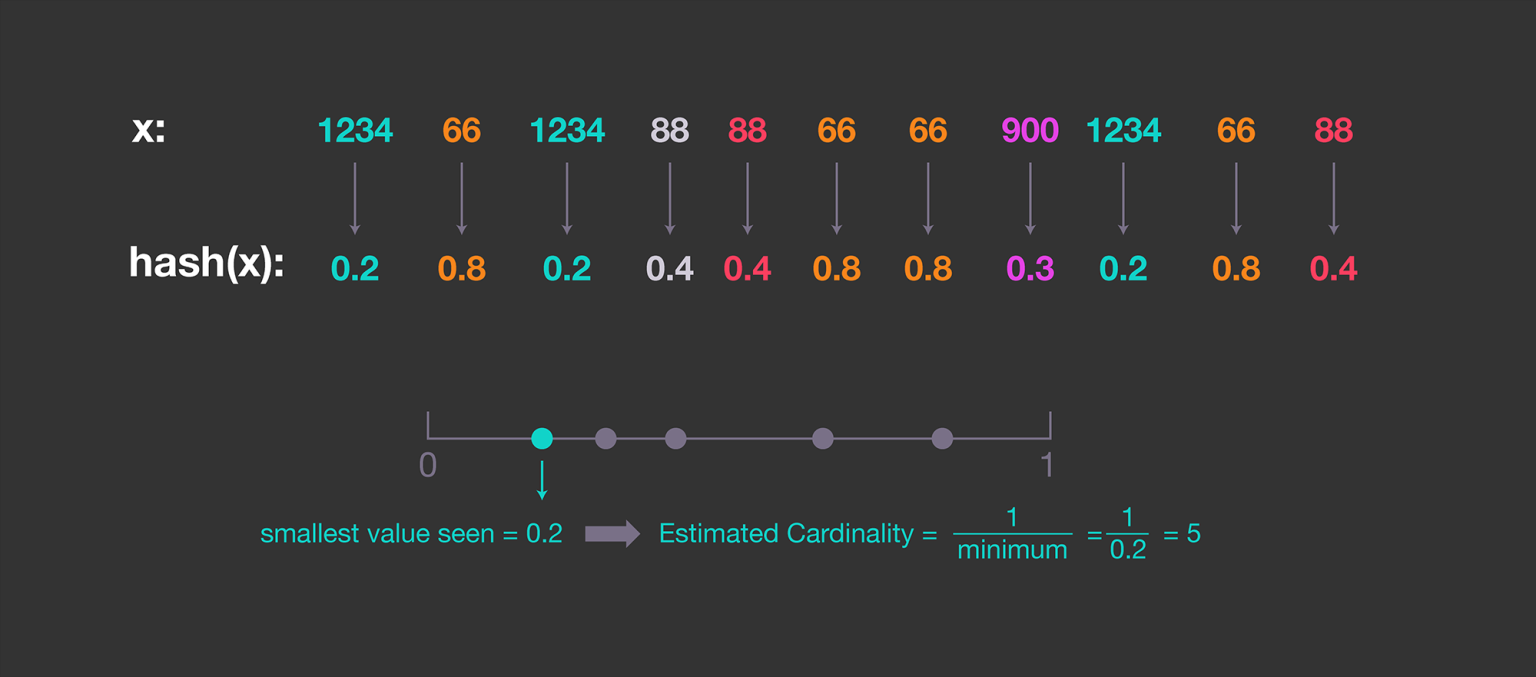
위 그림을 보면 간단히 이해할 수 있다.

  1. 0부터 1사이에서 균등한 간격으로 n개의 값들을 추출한다.
  2. 각 데이터를 n개의 값 중에 랜덤한 값으로 mapping
  3. 2.의 과정에서 smallest value를 pick

이제 1/(smallest value)는 데이터셋 전체의 cardinality에 대한 approximation!

그러나, 이 방법은 직관적으로도 매우 높은 variance를 가질 수 밖에 없다.
극단적으로 딱 한 번의 시행에서 n개의 값 중 가장 낮은 값을 뽑으면 말도 안되는 추정이 나오게 될 것이다.

Probabilistic Counting

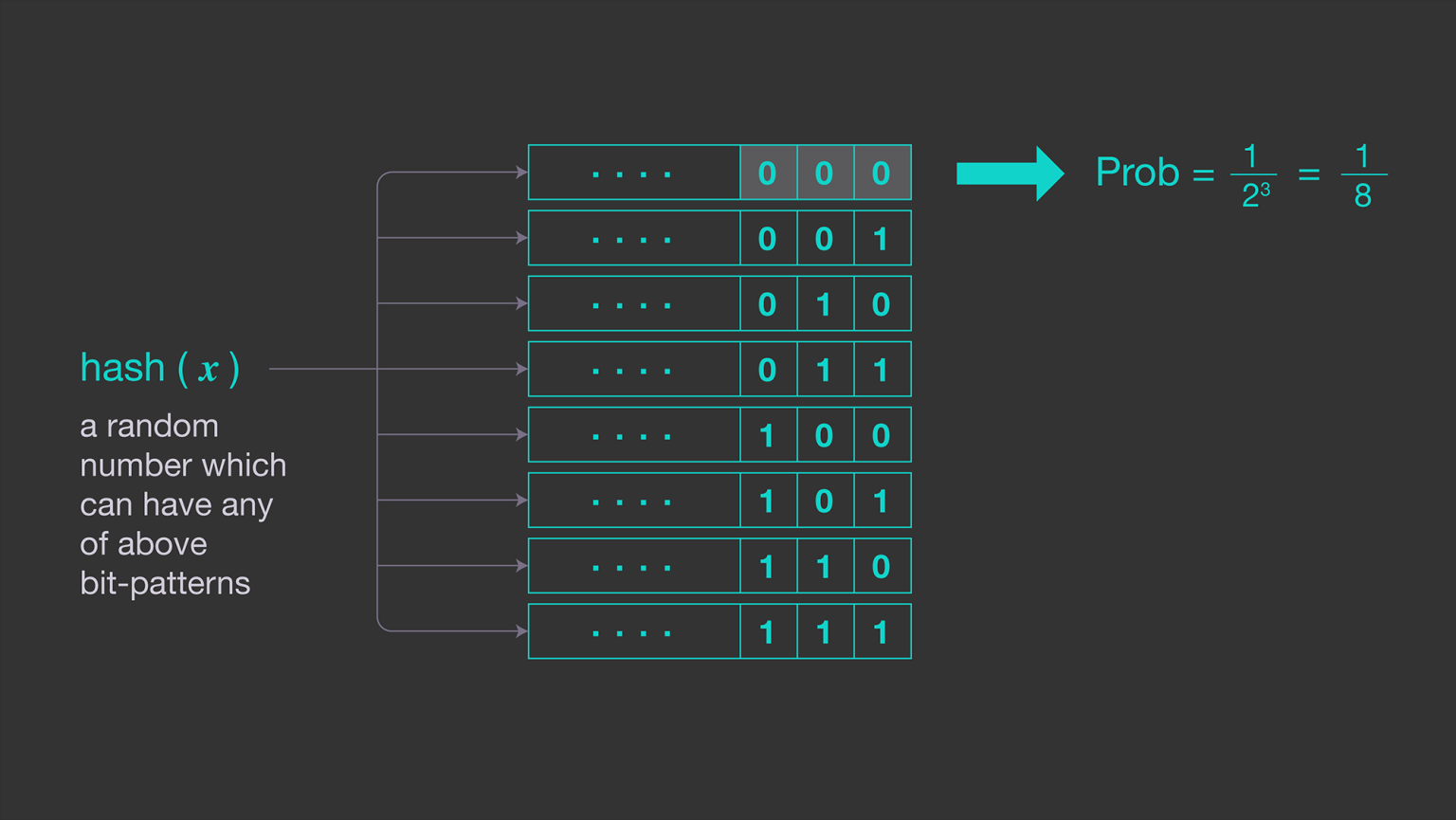
Simple estimator를 보완하기 위한 방법.
hash function을 통해 각 데이터에 대한 hash value를 얻은 뒤 hash value의 binary representation에서 consecutive zeros(연속된 0)의 개수를 센다.
이는 기본적으로 hash value가 n-consecutive zeros로 시작하는 binary일 확률은 12n\frac{1}{2^n}이기 때문이다.

다시 말하면 kk개의 연속된 0으로 시작하는(  ⟺  \iff leading 1이 k+1k+1-th entry에 등장하는) hash value는 2k2^k개의 데이터마다 하나씩 존재한다!
물론 이는 실제로도 반드시 그런다는 것이 아니라, 어디까지나 확률적으로 그렇게 추정할 수 있다는 것이다.
적어도 우리가 보는 bit의 상태는 0과 1 반반의 확률이니...

그러니 모든 데이터를 스캔하며 그저 hash value를 통해 maximum number of leading consecutive zeros를 기록하는 것으로 모든 것이 충분하다.

즉, 데이터 x1,x2,…,xnx_1, x_2, \dots, x_n으로부터 hash value의 연속된 0의 개수(MSB 혹은 LSB 둘 중 어디서부터 시작하건 상관 없다는 것도 알 수 있다.)를
ρ(x1),ρ(x2),…,ρ(xn)\rho(x_1), \rho(x_2), \dots, \rho(x_n)이라고 하자.
그러면 우리는 R=max⁡i=1,2,…,n{ρ(xi)}R=\max_{i=1,2, \dots ,n} \{\rho(x_i)\}을 얻을 수 있고, 이제 우리의 추정은 2R2^R.

간단히 생각해봐도 이러한 작업을 수행하는 동안 필요한 메모리는 1바이트 이상을 넘을 수가 없다. 최대 0의 개수만 기록하면 되기 때문이다.

다만 이 때 문제가 되는 부분은 두가지이다.

  1. 추정한 cardinality는 반드시 power of 2(2R2^R꼴)이다. 따라서 굉장히 rough한 형태로만 추정이 가능하다는 단점.
  2. 당연히 이번에도 variance가 높아질 것이다. 실은 simple estimator에 비해 무슨 장점이 있는지도 잘 모르겠다..

LogLog

상기했던 high variance를 해소하기 위해 우리는 여러 개의 estimator를 두어 평균을 취하는 접근법을 취할 것이다.
큰 수의 법칙이나 그런 이론적 근거를 생각해보지 않더라도 본능적으로 훨씬 더 안정적인 방법일 것임은 자명하다.

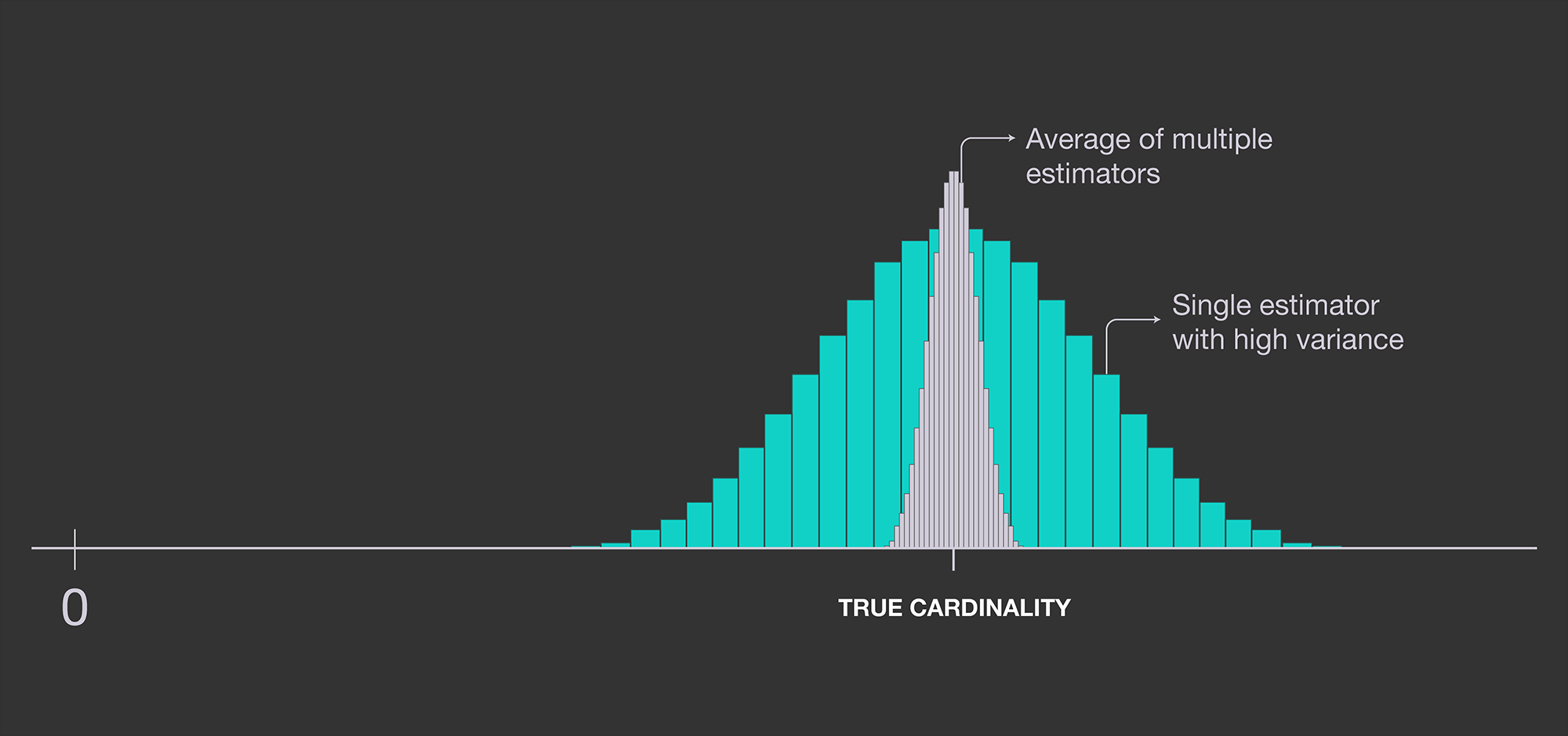
직관적인 접근법은 말 그대로 여러 개의 hash function을 정의하여 각 데이터마다 계산하는 것이다. 다만, 이는 (estimator의 개수) ×\times (처리할 데이터의 개수) 만큼의 계산을 필요로 하기 때문에 상황에 따라 computationally expensive할 수 있다.

여기서 정말 기가 막히는 방법을 어떤 위인들이 생각해내는데, hash value의 binary representation을 두 개의 부분으로 분리하는 것이다.

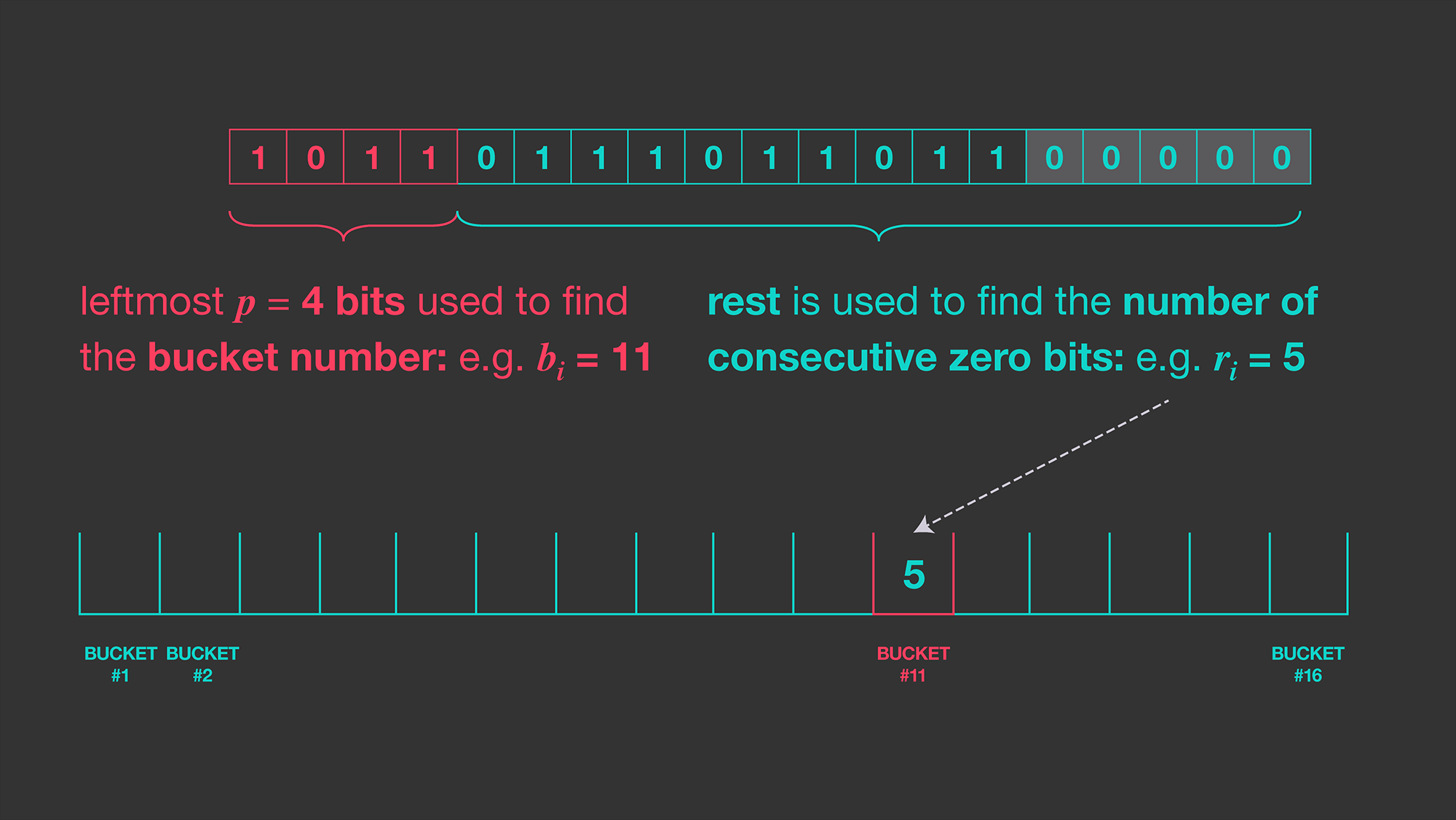
무슨 말인고 하면 상위(MSB 부분) pp-bit를 index, 나머지 하위 bit 부분을 consecutive zeros를 count하기 위한 부분으로 분리하겠다는 것이다.
이제 2p2^p 개의 resister(=bucket)을 생성한 뒤에 index를 통해 각 데이터의 consecutive zeros를 랜덤한 resister에 기록한다.

이러한 방법을 통해 우리는 2p2^p개의 각 resister에 기록된 가장 긴 consecutive zeros의 개수 R1,R2,…,R2pR_1, R_2, \dots, R_{2^p}를 구할 수 있으니,
각 resister에서 추정한 cardinality는 2R1,2R2,…,2R2p2^{R_1}, 2^{R_2}, \dots, 2^{R_{2^p}}.

이제 이러한 cardinality들의 기하평균을 구하여 resister 개수만큼 구하면 최종 cardinality를 추정할 수 있다.

CARDINALITYLogLog=constant⋅2p⋅212p∑i=12pRi\text{CARDINALITY}_\text{LogLog} = \text{constant} \cdot 2^p \cdot 2^{\frac{1}{2^p} \sum^{2^p}_{i=1} R_{i}}

이 때 constant\text{constant}는 편향을 보정하기 위한 보정치로 보통 0.794020.79402라고 한다.

이러한 알고리즘을 통해 2p2^p resister의 저장소만이 필요하고 각 resister의 크기는 1byte를 넘을 필요가 거의 없다.
저자들에 의하면, m=2pm=2^p resister를 통해 추정한 값의 표준편차가 약 1.3/m1.3/\sqrt{m}라고 한다.
211=20482^{11}=2048개의 resister를 설정하고 각 resister의 크기를 5-bit로 설정할 경우 2kbyte의 메모리 공간과 선형 시간복잡도 만으로도
최대 2272^{27}개까지 cardinality를 추정가능하며 이 때 평균적인 오차는 2.8퍼센트에 불과하다.

HyperLogLog

현재 Cardinality를 추정하는 SOTA 알고리즘은 HyperLogLog이다.

  1. LogLog 기법은 outlier에 큰 영향을 받는다고 한다. 저자들에 의하면, outlier를 제거하기 위해 하위 70퍼센트의 estimator만 계산할 경우 정확성이 1.05/m1.05/\sqrt{m}까지 향상되었다고 한다.
  2. 기하평균이 아닌 조화평균(harmonic mean)을 이용해 추정할 때 약간 더 정확한(1.04/m1.04/\sqrt{m}) 추정치를 얻을 수 있었다고 한다.
CARDINALITYHyperLogLog=constant⋅2p⋅2p2−R1+2−R2+⋯+2R2p\text{CARDINALITY}_\text{HyperLogLog} = \text{constant} \cdot 2^p \cdot \frac{2^p}{2^{-R_1} + 2^{-R_2} + \dots + 2^{R_{2^p}}}

이 때 상수 constant\text{constant}는 LogLog와 동일.

참고

Discuss on Twitter • View on GitHub